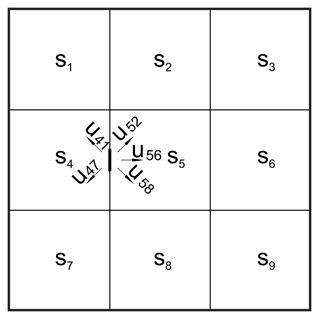
Stiffness coefficients and transfer indices of each slab depend on its type of support and its aspect ratio. These data are provided by tables in several books, e.g. by Hahn.
All supports are considered fixed when principal moments are calculated.
One support is freed, e.g. 45 of the figure, and distribution takes place on all directions (i.e. CROSS method on plane).
This procedure is repeated until moments balance.
Such a solution is, certainly, complex and laborious, but it is applicable in case of large spans with significant differences in dimensions and thicknesses.