So far, all the calculations depended on the structure geometry and were not affected by the magnitude of the external loading. For instance the centre of stiffness, the structural eccentricities, and the torsional radii, are independent of the seismic force magnitude.
Next, the displacements and stress resultants of the structure, due to external seismic loading H, will be calculated.
The relevant seismic force H is applied at the centre of mass CM of the diaphragm. This force is resolved in two forces Hx and Hy parallel to the two axes of the principal system. In order to apply the previous analysis, the forces Hx, Hy are transferred to the centre of stiffness CT together with the moment MCT according to the expression:

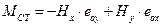 (9)
(9)
Example C.7-1: Given a horizontal force in x direction equal to is H=90.6 kN, carry-out the analysis of the structure.
Calculation of moment MCT :
The structural eccentricities are eox =-0.626 and eoy= yCM=-2.334m
For a given force Η=HX=90.6 kN in the initial system X0Y, the equivalent loading in the principal system (a=22.44ο) is: Hx=HX·cosa=90.6·0.924=83.72 kN and Hy=-HX·sina=-90.6·0.382=-34.64 kN and
ΜCT=-Hx·eoy+Hy·eox=-83.72kN·(-2.334m)+[-34.64kN·(-0.626m)]=195.4 kNm+21.7kNm=217.1 kNm
The following quantities are calculated using the Hx, Hy, MCT:
· the displacements δxo, δyo and θz of CT using the expressions:

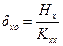 ,
, 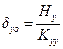
 ,
, 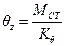
 (10)
(10)
where 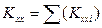
 ,
, 
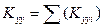 ,
, 
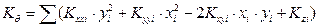
Example C.7-2:
Quantities Kxx=Σ(Kxxi)= 161.2·106N/m, Kyy=Σ(Kyyi)= 161.2·106 N/m and Κθ=3134·106 N·m are already calculated therefore:
δxo=Hx/Κxx =83.72·103N/(274.41·106N/m)=0.305 mm,
δyo=Hy/Κyy =-34.46·103N/(161.2·106 N/m)=- 0.214 mm and
θz=MCT/Kθ=217.1kNm/(3134·103kNm)=0.692·10-4
· the displacements δxi, δyi of the top of each column using the expressions:
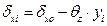
 ,
, 
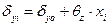 (11)
(11)
· and the displacements δζi, δηi by transferring δxi, δyi to the local system of each column using the expressions:

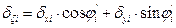 ,
, 
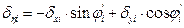 where
where 
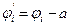 (12)
(12)
Example C.7-3:
C1: δx1= δxo- θz·y1=0.305mm-0.692·10-4·(-3.50·103mm)=(0.305+0.242)mm=0.547 mm
δy1= δyo+ θz·x1=-0.214mm+0.692·10-4·(-4.35·103mm)=(-0.214-0.301)mm=-0.515 mm
By transferring to the local system where φ’1=0.0-22.44°=-22.44°.
δζ1= δx1·cosφ’1+δy1·sinφ’1=0.547·0.924-0.515·(-0.382)=0.505+0.197=0.702 mm
δη1=-δx1·sinφ’1+δy1·cosφ’1=-0.547·(-0.382)+(-0.515)·0.924=0.209-0.476=-0.267 mm
C2: δx2= δxo- θz·y2=0.305mm-0.692·10-4·(-5.79·103mm)=(0.305+0.400)mm=0.705 mm
δy2= δyo+ θz·x2=-0.214mm+0.692·10-4·1.19·103mm=(-0.214+0.082)mm=-0.132 mm
By transferring to the local system where φ’2=0.0-22.44°=-22.4°.
δζ2= δx2·cosφ’2+δy2·sinφ’2=0.705·0.924+(-0.291)·(-0.132)=0.652+0.038=0.701 mm
δη2=-δx2·sinφ’2+δy2·cosφ’2=-0.705·(-0.382)+(-0.132)·0.924=0.269-0.122=0.147 mm
C3: δx3= δxo- θz·y3=0.305mm-0.692·10-4·1.12·103mm=(0.305-0.078)mm=0.227 mm
δy3= δyo+ θz·x3=-0.214mm+0.692·10-4·(-2.44·103mm)=(-0.214-0.169)mm=-0.383 mm
By transferring to the local system where φ’3=30.0-22.44°=7.56°.
δζ3= δx3·cosφ’3+δy3·sinφ’3=0.227·0.991+(-0.383)·0.132=0.225-0.050=0.175 mm
δη3=-δx3·sinφ’3+δy3·cosφ’3=-0.227·0.132+(-0.383)·0.991=-0.030-0.380=-0.410 mm
C4: δx4= δxo- θz·y4=0.305mm-0.692·10-4·(-1.17·103mm)=(0.305+0.081)mm=0.386 mm
δy4= δyo+ θz·x4=-0.214mm+0.692·10-4·3.10·103mm=(-0.214+0.215)mm=0.001 mm
By transferring to the local system where φ’4=45.0-22.44°=22.56°.
δζ4= δx4·cosφ’4+δy4·sinφ’4=0.386·0.923+0.001·0.384=0.355+0.000=0.355 mm
δη4=-δx4·sinφ’4+δy4·cosφ’4=-0.386·0.384+0.001·0.923=-0.148+0.001=-0.147 mm
In the example considered, for seismic action in X direction, the deformation due to rotation at column C2 gives δx2,θ=0.400 mm, higher than the deformation due to translation δxo=0.305 mm. The total displacement is therefore δx2=0.305+0.400=0.705 mm.
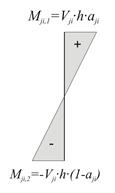 Figure C.7: Moment distribution (Mji,1- Mji,2=Vji·h)
Figure C.7: Moment distribution (Mji,1- Mji,2=Vji·h)
·  shear forces and bending moments of each column in its local system based on the relationships
shear forces and bending moments of each column in its local system based on the relationships
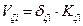
 ,
, 
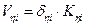 (13)
(13)
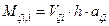 ,
, 
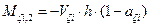 (14)
(14)
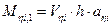
 ,
, 
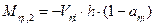
Example C.7-4:
Calculation of shear forces and bending moments :
The moment distribution factor is assumed the same in both directions aζi=aηi=0.50
C1: Vζ1=δζ1·Kζ1=0.702mm·31.1·106 N/m =21.8 kN
Vη1=δη1·Kη1=-0.267mm·31.1·106 N/m =-8.3 kN
Mζ1,1 =Vζ1·h·0.50=21.8·3.0·0.50=32.7 kNm Mζ1,2=- Mζ1,1=-32.7 kNm
Mη1,1=Vη1·h·0.50=-8.3·3.0·0.50=-12.5 kNm Mηι,2=- Mη1,1=12.5 kNm
C2: Vζ2=δζ2·Kζ2=0.701mm·31.1·106 N/m =21.8 kN
Vη2=δη2·Kη2=0.147mm·31.1·106 N/m =4.6 kN
Mζ2,1=Vζ2·h·0.50=21.8·3.0·0.50=32.7 kNm Mζ2,2=- Mζ2,1=-32.7 kNm
Mη2,1=Vη2·h·0.50=4.6·3.0·0.50=6.9 kNm Mη2,2=- Mη2,1=-6.9 kNm
C3: Vζ3=δζ3·Kζ3=0.175mm·186.6·106 N/m =32.7 kN
Vη3=δη3·Kη3=-0.410mm·26.2·106 N/m =-10.8 kN
Mζ3,1=Vζ3·h·0.50=32.7·3.0·0.50=49.1 kNm Mζ3,2=- Mζ3,1=-49.1 kNm
Mη3,1=Vη3·h·0.50=-10.8·3.0·0.50=-16.2 kNm Mη3,2=- Mη3,1=16.2 kNm
C4: Vζ4=δζ4·Kζ4=0.355mm·19.7·106 N/m =7.0 kN
Vη4=δη4·Kη2=-0.147mm·78.7·106 N/m =-11.6 kN
Mζ4=Vζ4·h·0.50=7.0·3.0·0.50=10.5 kNm Mζ4,2=- Mζ4,1=-10.5 kNm
Mη4,1=Vη4·h·0.50=-11.6·0·0.50=-17.4 kNm Mη4,2=- Mη4,1=17.4 kNm