Appendix D

GThe structural frame with 6 levels, project <B_d1>

In appendix Β’, the crossbar was used to assess the behaviour of the multistorey plane frame.
In this chapter, the composition of space frames, through beams and slabs, is considered. The diaphragm is the structural unit for the assessment of coupled space frames.

A diaphragm is the horizontal part of the floor consisting of slabs, connecting beams and columns. A floor may comprise more than one diaphragm, as shown in the example building of the present paragraph.

 

The most characteristic point of the diaphragm is the centre of stiffness.

 

The centre of stiffness C_T of a specific floor diaphragm is defined as the point about which the diaphragm rotates, under horizontal seismic force H.

The C_T point depends only on the geometry of the floor and is independent of the loadings, meaning that regardless the magnitude of the force, which may become equal to 2H, or 3H, or any other value, the centre of stiffness will remain the same. Of course, it depends on the geometry of the overlying and the underlying floors.

 

Principal axis system of diaphragm

is defined as the orthogonal axis system xC_Ty, in which when a horizontal seismic force H is applied on C_T, along axis x (or y), it results in translating C_T only along axis x (or y respectively). The angle a of the principal system, as to the initial system X0Y, is called principal angle of the diaphragm.

 

The above diaphragm data as well as the torsional stiffness K_θ and torsional ellipse stiffness ellipse (C_T, r_x, r_y), should be calculated in a general way. The method to be used should deal with more than one diaphragm per floor. Moreover, the general solution should account for the influence of non-diaphragmatic frames as well as the uneven level foundation. All possible special cases met in practice are included in the example presented in this paragraph, except for foundations, just for simplification reasons. Full scale analysis (including the foundation), can be performed by the engineer using the related software.

The behaviour of diaphragm on the left at the 5^th level, analysed next is directly affected by the L-type frame C₂₁-C₂₆-C₂₇-C₂₈ connected to it and indirectly by column C₆ and the diaphragm on the right, through the frames of other floors.

A general method for the calculation of the diaphragm data is presented next.

This method creates a condition allowing the diaphragm only to rotate about the centre of stiffness C_T, which remains stationary with respect to the ground.

The method comprises four steps, the first three of which include a space frame analysis.

Loading: Force H_X=100 and moment M_CM,X on centre of mass C_M of diaphragm i
Results: total displacements of structure and displacements of diaphragm i

The two displacements δ_XX1, δ_XY1 of point 1 of diaphragm i and its angle θ_XZ are required.

Any value may be given to force H_Χ, as long as it is the same for the analyses of the three first steps. In this example, H_Χ is given equal to 100 kN. The application point of force H is irrelevant, but for higher accuracy in calculations, the force is assumed applied at an arbitrary eccentricity c_y, e.g. 2.0 m, in relation to the centre of mass, in order to produce a significant rotation of the diaphragm and thus achieve a higher accuracy in the calculations. That eccentricity is essential, especially in cases where the centre of stiffness is close or coincides with the centre of mass. Therefore, in addition to force H_Χ, moment M_CM,x=100kN×2.00m= 200 kNm is also applied at C_M.

Point 1 corresponds to column Κ2 joint, but could be any point of the diaphragm.

The only results needed from this analysis are the translations of point 1 δ_XX1=2.681 mm, δ_XY1=-0.231 mm and the angle θ_XZ=4.5613×10^-5 of the diaphragm. The displacements of point 2 will be used only to verify the generality of the method.

All displacements are absolute with respect to the ground.

Loading: H_X=100 on diaphragm i with rotational restraint

Results: the total displacements of structure and the two parallel translations of diaphragm

 

The two translations of point 1 δ_XXo, δ_XYo, are only required, being identical for any point of the diaphragm i, thus also for C_T, since the angle of rotation of the diaphragm is zero.

All diaphragm points, thus also CT, have identical displacements

Diaphragm is restrained against rotation, therefore θ_XZ=0

Due to zero rotation of diaphragm i, point 1 has only two parallel translations, δ_XXo=2.103 mm and δ_XYo=-0.047mm, being identical for all diaphragm points, thus also for C_T. In other diaphragms located in the same, upper or lower level, small, yet measurable rotations exist, thus every point on them has different displacements.

 

Loading: H_Y=100 on diaphragm i with rotational restraint
Results: the total displacements of structure and the two parallel translations of diaphragm

The two translations of point 1 δ_XXo, δ_XYo, are only required, being identical for any point of the diaphragm i, thus also for C_T, provided that the angle of rotation of the diaphragm is zero.

 

All diaphragm points, thus also C_T, have identical displacements

Diaphragm is restrained against rotation, therefore θ_XZ=0

Due to zero rotation of diaphragm i, point 1 has only two parallel translations, δ_YXo=-0.047 and δ_YYo=1.668 mm, being identical for all diaphragm points, thus also for C_T. As in step 2, in other diaphragms located in the same, upper or lower level small, yet measurable rotations exist, thus every point on them has different displacements.

The secondary displacements δ_XYo of loading 1 and δ_YXo of loading 3 are always equal, i.e.  δ_XYo=δ_YXo should always derive from the space frame analysis.

Analysis 3 is performed only to obtain translation δ_YYo needed for the calculation of angle a of the principal system.

The angle a of the principal system of diaphragm i is calculated by means of the equation C.9.1 of §C.9 using the 2^nd and 3^rd analysis results:

tan(2a)=2δ_XYo/(δ_XXo-δ_YYo)=2×(-0.047)/(2.103-1.668)=-0216 → 2a=-12.2º → a=-6.1º

 

The only load acting on diaphragm i is moment on C_T

Diaphragm displacements are induced only due to rotation

The centre of stiffness C_T remains stationary with respect to the ground

 

Using this trick, namely by subtracting analysis 2 results from analysis 1 results, the diaphragm i develops only rotation, while the remaining diaphragms develop both translations and rotation. However only diaphragm i is examined here. The most important result of this trick is that the diaphragm i is rotated about C_T, which remains stationary with respect to the ground, allowing the calculation of its precise location. The rotation angle of diaphragm i is the rotation angle θ_XZ calculated in step 1 under the corresponding loading.

The displacements of an arbitrary point j of the diaphragm, due to rotation θ_XZ derive form the expressions:

δ_Χtj=δ_XXj-δ_XXo, δ_Ytj=δ_XYj-δ_XYo

The C_T coordinates corresponding to these displacements are:

X_CT=X_j-δ_Ytj/θ_XZ

Y_CT=Y_j+δ_Xtj/θ_XZ

In the example considered, for point 1:

δ_Χt1=δ_XX1-δ_XXo=2.681-2.103=0.578 mm

δ_Yt1=δ_XY1-δ_XYo=-0.211-(-0.047)=-0.164 mm

The diaphragm rotation is identical to that of analysis 1, i.e. θ_XZ=4.5613·10^-5.

The coordinates of point 1 are (6.0, 0.0), thus:

X_CT=X₁-δ_Yt1/θ_XZ=6.0-(-0.164)·10^-3/(4.5613·10^-5)=9.6 m

Y_CT=Y₁+δ_Xt1/_θXZ=0.0+0.578·10^-3/(4.5613·10^-5)=12.7 m

 

Each diaphragm has two lateral stiffnesses in the two principal directions.

Lateral stiffness of diaphragm K_xx (or K_yy) along the principal x (or y) direction, is defined as the ratio of the seismic force H to the corresponding δ_xo (or δ_yo) displacement of the diaphragm, when force acts on C_T along the principal direction considered, i.e.:

K_xx=H_xx/δ_xxo , K_yy=H_xy/δ_xyo or equivalent:  K_xx=H_yx/δ_yxo , K_yy=H_yy/δ_yyo

Using analysis 2, the external force H_X=100 of the initial system X0Y is resolved into two equivalent principal forces H_xx=100·cosa and H_xy=-100·sina (see §C.2) acting in x,y directions of the principal system. In the present case, a=-6.154º, therefore H_xx=100·0.994=99.4 kN and H_xy=-100·(-0.107)=10.7 kN.

Respectively, the two translations of the centre of stiffness in X0Y, derived from analysis 2, are δ_XXo=2.103, δ_ΧΥο=-0.047, which transferred in the principal system yield (§C.2):

δ_xxo=δ_XXo·cosa-δ_XYo·sina=2.103·0.994-(-0.047)·(-0.107)=2.090-0.005=2.085 mm

δ_xyo=-δ_XXo·sina+δ_XYo·cosa=-2.103·(-0.107)+(-0.047)·0.994=0.225-0.047=0.178 mm→

K_xx=H_xx/δ_xxo=99.4·10³N/2.085·10^-3m=47.7·10⁶ N/m

K_yy=H_xy/δ_xyo=10.7·10³N/0.178·10^-3m=60.1·10⁶ N/m

Torsional stiffness of diaphragm K_θ is defined as the ratio of moment M_CT acting on the centre of stiffness C_T, to the rotation angle θ_z of the diaphragm.

Moment acting on C_T is equal to

M_XCT=100.0·(Y_CT-Y_CM)+100.0·c_Y=100·(12.685-12.323)+200.0=36.2+200.0=236.2 kNm

K_θ=M_XCT/θ_XZ=236.2·10³Nm/4.5613·10^-5=5178·10⁶  Nm

Torsional stiffness distribution of diaphragm is the curve on which, if the idealised columns with the same lateral stiffnesses as those of the diaphragm, are placed symmetrically with respect of the centre of stiffness, the torsional stiffness derived is the same as that of the diaphragm.

Torsional stiffness ellipse of diaphragm is defined as the ellipse having C_T as centre and r_x=√(K_θ/K_yy), r_y=√(K_θ/K_xx) as radii.

r_x=√K_θ/K_yy=√[5178×10⁶Νm/60.1×10⁶N/m]=9.28 m
r_y=√K_θ/K_xx=√[5178×10⁶Nm/47.7×10⁶N/m]=10.42 m

 

The equivalent building should comprise same number of floors and diaphragms. The columns of each floor should have specific dimensions, thus for each floor relative lateral and torsional stiffnesses are used.

Each diaphragm is replaced by an equivalent one consisting of 4 fixed-ended columns placed symmetrically with respect to its centre of stiffness.

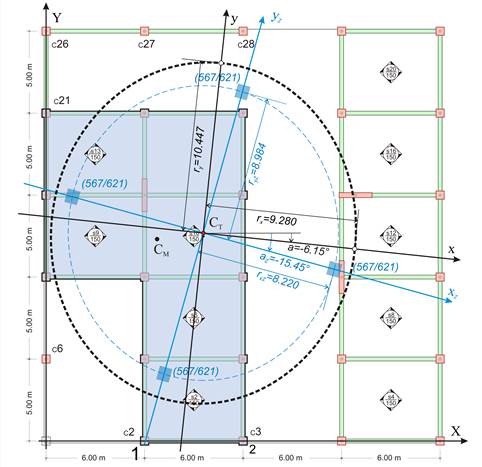
The equivalent diaphragm i is assumed to behave as an one-storey structure of fixed-ended columns. The four relative translations of the centre of stiffness along X, Y axes δ_XXoΖ,i, δ_XYoΖ,i , δ_YXoΖ,i, δ_YYoΖ,i  as well as the rotation angle θ_XZMZ,I are defined as functions of the actual building displacements as follow.

δ_XXoΖ,i= δ_XXo,i-δ_XXo,i-1 , δ_XYoΖ,i=δ_XYo,i-δ_XYo,i-1 ,
δ_YXoΖ,i= δ_YXo,i-δ_YXo,i-1,  δ_YYoΖ,i=δ_YYo,i-δ_YYo,i-1,
θ_XZΜZ,i = θ_XΖΜ,i –θ_XZΜ,i-1.

Therefore, the data of the equivalent diaphragm are: rotation angle a_z,i=2δ_XYoΖ,i/( δ_XXoΖ,i- δ_YYoΖ,i),

torsional stiffness K_θZ,i=H·c_Y/ θ_XZΜZ,i , lateral stiffnesses K_xxZ,i= H/(δ_XXoZ,i+δ_XYoZ,i·tana_Z,i) και K_yyΖ,ι=H/(δ_YYoZ,i-δ_XYoZ,i·tana_Z,i) (equations C.9.2 and C.9.3 of §C.9).

Also r_xZ,i=√K_θZ,i/K_yyZ,i, r_yZ,i=√K_θZ,i/K_xxZ,i

The location of the equivalent diaphragms is determined by translating the centre of stiffness to point 0.0, 0.0. In this way the equivalent building is created and for its diaphragms i the following relations apply:

δ_{XXo_equal,i}=Σ(δ_XXoΖ,k) όπου k=i έως 1 à δ_{XXo_equal,i}=Σ(δ_XXo,i-δ_XXo,i-1)= (δ_XXo,i-δ_XXo,i-1)+ (δ_XXo,i-1-δ_XXo,i-2)+…+ (δ_XXo,1-0.0)=δ_XXo,i à δ_{XXo_equal,i}=δ_XXo,i

Using the same logic δ_{XYo_equal,i}=δ_XYo,i , δ_{YYo_equal,i}=δ_YYo,i και  θ_{XZ_equal,i}= θ_XZΜ,i

Therefore all diaphragm quantities K_{xx_equal,i} , K_{yy_equal,i} , K_{θ_equal,i} are equal to those of the actual building.

The seismic assessment of the actual building can be performed in an easy, direct and descriptive way by means of the equivalent building.