Span moments of two-way slabs, are relatively low (Mx=8.9 kNm and My=4.9 kNm), compared to the respective values of the 1st example (10.8 and 4.1 kNm).
At the common support, Mx,erm=-20.0 kNm (the respective value of the 1st example: -22.0 kNm), whereas at the border with the three-edge-supported slabs is My,erm=-17.4 kNm (the respective value of the 1st example: -16.2 kNm).
It is concluded that the stress resultants on most of the area of the two-way slabs are similar to those of the 1st example.
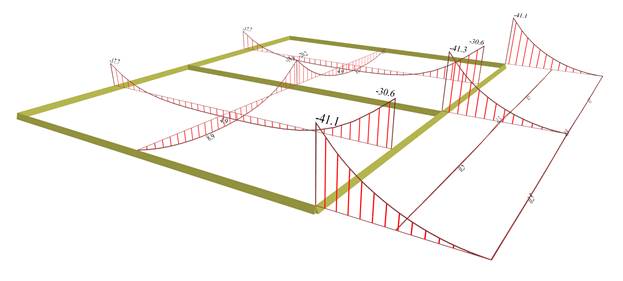
In the region of the continuity with the cantilever support moments are -30.6 kNm equal to almost isostatic moment of the cantilever. The higher moments of the cantilever - 41.0 kNm are the local peak moments, as shown in the next figure in the detailed distribution of the My due to the fixed transverse supports.