Έως εδώ όλοι οι υπολογισμοί εξαρτιόνταν από τη γεωμετρία του φορέα και δεν επηρεάζονταν από το μέγεθος της εξωτερικής φόρτισης, π.χ. το Κέντρο Ελαστικής Στροφής, οι στατικές εκκεντρότητες, ή οι ακτίνες δυστρεψίας, είναι ανεξάρτητες του μεγέθους της σεισμικής δύναμης.
Στη συνέχεια θα υπολογίσουμε τις παραμορφώσεις του φορέα και τις εντάσεις του λόγω της εξωτερικής σεισμικής φόρτισης H.
Η εκάστοτε σεισμική δύναμη H εξασκείται στο κέντρο μάζας CM του διαφράγματος. Η δύναμη αυτή μπορεί να αναλυθεί στις δύο δυνάμεις Hx και Hy παράλληλα στους δύο άξονες του κύριου συστήματος. Για να μπορέσουμε να εφαρμόσουμε την προηγούμενη ανάλυση, μεταφέρουμε τις δυνάμεις Hx, Hy στο κέντρο ελαστικής στροφής CT μαζί με τη ροπή MCT βάσει της σχέσης:

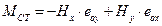 (9)
(9)
Παράδειγμα Γ.7-1: Αν η οριζόντια δύναμη κατά x είναι H=90.6 kN, ζητείται η επίλυση του φορέα.
Υπολογισμός ροπής MCT :
Οι στατικές εκκεντρότητες είναι eox =-0.626 και eoy= yCM=-2.334m
Για δύναμη Η=HX=90.6 kN στο αρχικό σύστημα X0Y θα έχουμε στο κύριο σύστημα (a=22.44ο) την ισοδύναμη φόρτιση Hx=HX·cosa=90.6·0.924=83.72 kN και Hy=-HX·sina=-90.6·0.382=-34.64 kN και
ΜCT=-Hx·eoy+Hy·eox=-83.72kN·(-2.334m)+[-34.64kN·(-0.626m)]=195.4 kNm+21.7kNm=217.1 kNm
Με τα εξωτερικά μεγέθη Hx, Hy, MCT, υπολογίζουμε:
· τις παραμορφώσεις δxo, δyo και θz του πόλου περιστροφής του διαφράγματος από τις σχέσεις:

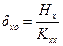 ,
, 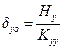
 ,
, 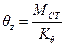
 (10)
(10)
όπου 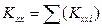
 ,
, 
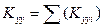 ,
, 
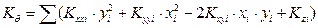
Παράδειγμα Γ.7-2:
Έχουν ήδη υπολογιστεί Kxx=Σ(Kxxi)= 161.2·106N/m, Kyy=Σ(Kyyi)= 161.2·106 N/m και Κθ=3134·106 N·m οπότε
δxo=Hx/Κxx =83.72·103N/(274.41·106N/m)=0.305 mm,
δyo=Hy/Κyy =-34.46·103N/(161.2·106 N/m)=- 0.214 mm και
θz=MCT/Kθ=217.1kNm/(3134·103kNm)=0.692·10-4
· τις παραμορφώσεις δxi, δyi της κεφαλής κάθε κολόνας από τις σχέσεις:
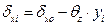
 ,
, 
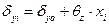 (11)
(11)
· and the displacements δζi, δηi by transferring δxi, δyi to the local system of each column using the expressions:

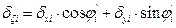 ,
, 
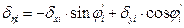 όπου
όπου 
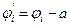 (12)
(12)
Παράδειγμα Γ.7-3:
C1: δx1= δxo- θz·y1=0.305mm-0.692·10-4·(-3.50·103mm)=(0.305+0.242)mm=0.547 mm
δy1= δyo+ θz·x1=-0.214mm+0.692·10-4·(-4.35·103mm)=(-0.214-0.301)mm=-0.515 mm
Και με μεταφορά στο τοπικό σύστημα που φ’1=0.0-22.44°=-22.44°.
δζ1= δx1·cosφ’1+δy1·sinφ’1=0.547·0.924-0.515·(-0.382)=0.505+0.197=0.702 mm
δη1=-δx1·sinφ’1+δy1·cosφ’1=-0.547·(-0.382)+(-0.515)·0.924=0.209-0.476=-0.267 mm
C2: δx2= δxo- θz·y2=0.305mm-0.692·10-4·(-5.79·103mm)=(0.305+0.400)mm=0.705 mm
δy2= δyo+ θz·x2=-0.214mm+0.692·10-4·1.19·103mm=(-0.214+0.082)mm=-0.132 mm
Και με μεταφορά στο τοπικό σύστημα που φ’2=0.0-22.44°=-22.4°.
δζ2= δx2·cosφ’2+δy2·sinφ’2=0.705·0.924+(-0.291)·(-0.132)=0.652+0.038=0.701 mm
δη2=-δx2·sinφ’2+δy2·cosφ’2=-0.705·(-0.382)+(-0.132)·0.924=0.269-0.122=0.147 mm
C3: δx3= δxo- θz·y3=0.305mm-0.692·10-4·1.12·103mm=(0.305-0.078)mm=0.227 mm
δy3= δyo+ θz·x3=-0.214mm+0.692·10-4·(-2.44·103mm)=(-0.214-0.169)mm=-0.383 mm
Και με μεταφορά στο τοπικό σύστημα που φ’3=30.0-22.44°=7.56°.
δζ3= δx3·cosφ’3+δy3·sinφ’3=0.227·0.991+(-0.383)·0.132=0.225-0.050=0.175 mm
δη3=-δx3·sinφ’3+δy3·cosφ’3=-0.227·0.132+(-0.383)·0.991=-0.030-0.380=-0.410 mm
C4: δx4= δxo- θz·y4=0.305mm-0.692·10-4·(-1.17·103mm)=(0.305+0.081)mm=0.386 mm
δy4= δyo+ θz·x4=-0.214mm+0.692·10-4·3.10·103mm=(-0.214+0.215)mm=0.001 mm
Και με μεταφορά στο τοπικό σύστημα που φ’4=45.0-22.44°=22.56°.
δζ4= δx4·cosφ’4+δy4·sinφ’4=0.386·0.923+0.001·0.384=0.355+0.000=0.355 mm
δη4=-δx4·sinφ’4+δy4·cosφ’4=-0.386·0.384+0.001·0.923=-0.148+0.001=-0.147 mm
Στο συγκεκριμένο παράδειγμα όπου για σεισμό κατά X, η παραμόρφωση λόγω στροφής στη κολόνα C2 δίνει δx2,θ=0.400 mm που είναι μεγαλύτερη από τη μεταφορική παραμόρφωση δxo=0.305 mm και έτσι η συνολική παραμόρφωση γίνεται δx2=0.305+0.400=0.705 mm.
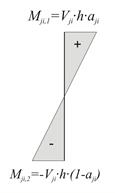 Εικόνα Γ.7: Κατανομή ροπών (Mji,1- Mji,2=Vji·h)
Εικόνα Γ.7: Κατανομή ροπών (Mji,1- Mji,2=Vji·h)
· τις τέμνουσες και τις ροπές κάθε υποστυλώματος στο τοπικό του σύστημα βάσει των σχέσεων:
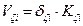
 ,
, 
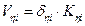 (13)
(13)
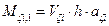 ,
, 
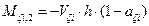 (14)
(14)
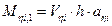
 ,
, 
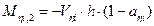
Παράδειγμα Γ.7-4:
Υπολογισμός τεμνουσών και ροπών :
Ο συντελεστής κατανομής των ροπών θα ληφθεί ίδιος και προς τις 2 διευθύνσεις aζi=aηi=0.50
C1: Vζ1=δζ1·Kζ1=0.702mm·31.1·106 N/m =21.8 kN
Vη1=δη1·Kη1=-0.267mm·31.1·106 N/m =-8.3 kN
Mζ1,1 =Vζ1·h·0.50=21.8·3.0·0.50=32.7 kNm Mζ1,2=- Mζ1,1=-32.7 kNm
Mη1,1=Vη1·h·0.50=-8.3·3.0·0.50=-12.5 kNm Mηι,2=- Mη1,1=12.5 kNm
C2: Vζ2=δζ2·Kζ2=0.701mm·31.1·106 N/m =21.8 kN
Vη2=δη2·Kη2=0.147mm·31.1·106 N/m =4.6 kN
Mζ2,1=Vζ2·h·0.50=21.8·3.0·0.50=32.7 kNm Mζ2,2=- Mζ2,1=-32.7 kNm
Mη2,1=Vη2·h·0.50=4.6·3.0·0.50=6.9 kNm Mη2,2=- Mη2,1=-6.9 kNm
C3: Vζ3=δζ3·Kζ3=0.175mm·186.6·106 N/m =32.7 kN
Vη3=δη3·Kη3=-0.410mm·26.2·106 N/m =-10.8 kN
Mζ3,1=Vζ3·h·0.50=32.7·3.0·0.50=49.1 kNm Mζ3,2=- Mζ3,1=-49.1 kNm
Mη3,1=Vη3·h·0.50=-10.8·3.0·0.50=-16.2 kNm Mη3,2=- Mη3,1=16.2 kNm
C4: Vζ4=δζ4·Kζ4=0.355mm·19.7·106 N/m =7.0 kN
Vη4=δη4·Kη2=-0.147mm·78.7·106 N/m =-11.6 kN
Mζ4=Vζ4·h·0.50=7.0·3.0·0.50=10.5 kNm Mζ4,2=- Mζ4,1=-10.5 kNm
Mη4,1=Vη4·h·0.50=-11.6·0·0.50=-17.4 kNm Mη4,2=- Mη4,1=17.4 kNm