Τριέρειστες είναι οι πλάκες που στηρίζονται σε τρεις παρυφές.
Η στατική επίλυση γίνεται με τρόπο ανάλογο αυτού των τετραερείστων πλακών (δηλαδή κάθε πλάκα μεμονωμένα), με τη βοήθεια πινάκων π.χ. του Hahn.
Αντίστοιχοι πίνακες με ελληνικές επεξηγήσεις υπάρχουν στο βιβλίο των Πινάκων με τίτλο “Εφαρμογές Οπλισμένου Σκυροδέματος” (σελίδες 46 έως 51 για τετραέρειστες, 52 έως 59 για τις τριέρειστες και τις διέρειστες) της σειράς των βιβλίων του Απόστολου Κωνσταντινίδη του 1994.
Οι ροπές κατανέμονται πρακτικά, με την προσεγγιστική μέθοδο της § 4.6.3.3.
Στους πίνακες υποστηρίζονται το καθολικό ομοιόμορφο φορτίο, το συνεχές γραμμικό ομοιόμορφο φορτίο στην ελεύθερη παρυφή και η συνεχής γραμμική ροπή στην ελεύθερη παρυφή.
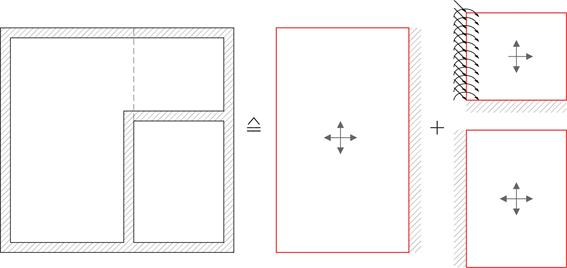
Μία πλάκα μορφής Γ επιλύεται προσεγγιστικά αναλύοντάς την σε μία τετραέρειστη και μία τριέρειστη, όπως φαίνεται στο σχήμα. Η μέθοδος αυτή προτείνεται από τον Hahn και απαιτεί ιδιαίτερη προσοχή στην όπλιση της πλάκας. Ενδεικτικά αναφέρουμε ότι θα πρέπει να διατάσσονται συνεχείς οπλισμοί και στις κάτω ίνες στο θεωρητικό όριο τετραέρειστης και τριέρειστης πλάκας.