Μηχανικό προσομοίωμα

l_eff=l_n+α_left+α_right  όπου  α=min(t/2,h/2)

· Στην ακραία στήριξη της πρώτης πλάκας, η θεώρηση πλάτους a=t₁/2=125 mm είναι αποδεκτή δεδομένου ότι, εκτός των άλλων είναι υπέρ της ασφαλείας.
· Στις στηρίξεις δοκών επί κολονών, τα πλάτη στήριξης λαμβάνονται υπόψη πιο αποτε-λεσματικά, όταν η ανάλυση γίνεται με χρήση των στερεών σωμάτων.

Συνεχής δοκός: l_o μήκος μεταξύ διαδοχικών σημείων μηδενισμού ροπών 

Συνεχής δοκός πλαισίων: l_o μήκος μεταξύ διαδοχικών σημείων μηδενισμού ροπών

Στις αντισεισμικές κατασκευές απαιτούνται ισχυρά υποστυλώματα και ακλόνητες συνδέσεις των δοκών με αυτά. Η ανάγκη αυτή δημιουργεί ένα σύνολο πλαισιακών δοκών, συνεχών ως προς τη γεωμετρία, αυτόνομων όμως σε μεγάλο βαθμό από τις γειτονικές και μας οδηγεί στο συμπέρασμα ότι η περίπτωση αρθρωτής δοκού είναι σπάνια. Έτσι, θα μπορούσαμε να επιλέξουμε l_o=0.70×l για όλες τις αντισεισμικές δοκούς.

b_eff=b_w+b_eff,1+b_eff,2≤b_lim όπου b_eff,1=0.20×b₁+0.10×l_o≤0.20×l_o και b_eff,2=0.20×b₂+0.10×l_o≤0.20×l_o.

· Τα συνεργαζόμενα πλάτη στις στηρίξεις έχουν πρακτικό νόημα κυρίως για τη διαστα-σιολόγηση σε κάμψη ανεστραμμένων πλακοδοκών.
· Σε περίπτωση που μια συντρέχουσα πλάκα είναι πρόβολος ανοίγματος l_n, τότε το ανάλογο b₁ ή b₂ ισούται με l_n.

Η πραγματική κατασκευή και η χωρική προσομοίωση (οθόνη από το εκπαιδευτικό λογισμικό)

Στο χωρικό προσομοίωμα μπορούμε να παρατηρήσουμε τόσο τους κόμβους(π.χ. κόμβος 1, 5, 9 κτλ.), όσο και τις ράβδους (π.χ. ράβδος 1, 2, 5 κτλ.). Ο κόμβοι είναι σημεία χωρίς διαστάσεις στα οποία καταλήγουν οι ράβδοι

Κάθε κόμβος έχει γενικά 6 μετακινήσεις (6 βαθμούς ελευθερίας), τρείς μετατοπίσεις  δ_x, δ_y, δ_z και τρεις στροφές φ_x, φ_y, φ_z. Το ζητούμενο σε μια επίλυση είναι να υπολογισθούν και οι 6 μετακινήσεις όλων των κόμβων.

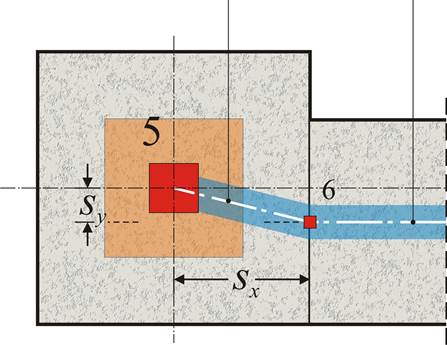
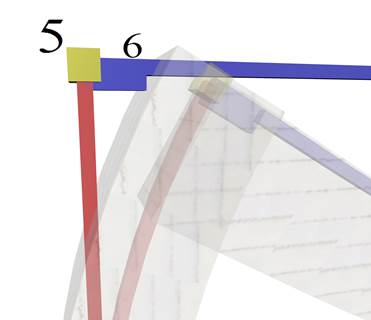
Κάτοψη και 3D κόμβων κολόνας δοκού
κύριος κόμβος  (5) και εξαρτημένος κόμβος (6)

Αν οι 6 μετακινήσεις του κύριου κόμβου είναι δ_x, δ_y, δ_z, φ_x, φ_y, φ_z, οι αντίστοιχες δ_x,s, δ_y,s, δ_z,s, φ_x,s, φ_y,s, φ_z,s του εξαρτημένου κόμβου είναι:

φ _x,s = φ _x , φ _y,s = φ _y , φ _z,s = φ _z , δ _x,s = δ _x -s_y × φ _z (δεδομένο: s_z=0), δ _y,s = δ _y +s_x × φ _z (δεδομένο: s_z=0),

δ _z,s = δ _z -s_x × φ _y +s_y × φ _x

Διαφραγματική λειτουργία ορόφου και οι παραμορφώσεις τυχόντος σημείου i του διαφράγματος λόγω φ_z

Οι τρεις μετακινήσεις δ_z, φ_x, φ_y κάθε κόμβου που ανήκουν στο διάφραγμα είναι ανεξάρτητες μεταξύ τους, ενώ οι άλλες τρεις δ_x, δ_y, φ_z είναι εξαρτημένες από τις τρεις μετακινήσεις του σημείου C_T που ονομάζεται Κέντρο Ελαστικής Στροφής του διαφράγματος.Σε ένα σημείο i του διαφράγματος οι δ_xi, δ_yi, φ_zi δίνονται από τις παρακάτω σχέσεις: