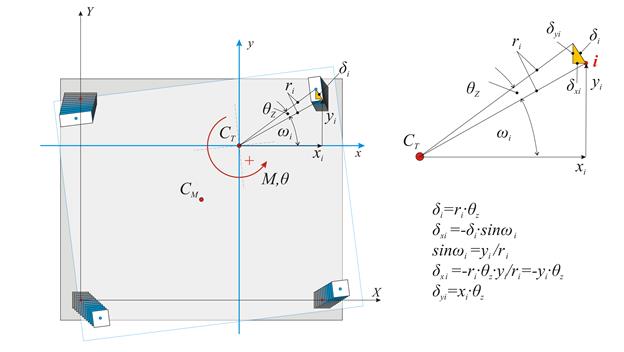
Εξετάζουμε την παραμόρφωση που προκαλεί η εξωτερική ροπή M, η οποία ασκείται στο κέντρο ελαστικής στροφήςCT. Προκειμένου να εξετάσουμε την κίνηση αυτή, μεταφερόμαστε
(απλή παράλληλη μετάθεση) από το αρχικό σύστημα X0Y στο κύριο σύστημα xCTy. Η μεταφορά του κέντρου μάζας στο κύριο σύστημα πραγματοποιείται με τις στατικές εκκεντρότητες [1] eox, eoy τουCM ως προς το CT σύμφωνα με τις σχέσεις:
Κύριο σύστημα συντεταγμένων
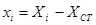 ,
,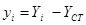 ,
,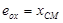 ,
, 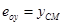 (6’)
(6’)
Η παραμόρφωση του διαφράγματος είναι ουσιαστικά μία στροφή θz περί το CT, η οποία προκαλεί μετατόπιση δi στην κεφαλή κάθε υποστυλώματος i με συντεταγμένες xi,yi ως προς το σύστημα συντεταγμένων με αρχή το CT. Αν η απόσταση του σημείου i από το CT ισούται με ri, οι δύο συνιστώσες της (απειροστής) παραμόρφωσης δi ισούνται με δxi=-θz·yi και δyi=θz·xi.
Οι μετατοπίσεις δxi, δyi δημιουργούν σε κάθε υποστύλωμα τέμνουσες Vxi και Vyi, όπου
Vxi=Kxi·δxi=Kxi·(-θz·yi) → Vxi=-θz·Kxi·yi και Vyi=Kyi·δyi=Kyi·(θz·xi) → Vyi=θz·kyi·xi
Η συνισταμένη των ροπών όλων των τεμνουσών δυνάμεων Vxi, Vyi ως προς το κέντρο ελαστικής στροφής ισούται με την εξωτερική ροπή MCT, δηλαδή
MCT=Σ(-Vxi·yi+Vyi·xi+Kzi) → MCT= θz·Σ(Kxi·yi2+Kyi·xi2+Kzi)
Δυστρεψία Kzi υποστυλώματος i
Οι κολόνες ανθίστανται στη στροφή του διαφράγματος με την καμπτική τους δυσκαμψία κατά τους όρους Kxi·yi2 , Kyi·xi2 (σε N·m), αλλά και με την ίδια τη δυστρεψία τους Kzi σε μονάδες ροπής π.χ. N·m.
Η δυστρεψία ενός υποστυλώματος ισούται με Kz=0.5E·Id/h, όπου 0.5Ε είναι το μέτρο διάτμησης G του υλικού, το οποίο συνήθως λαμβάνεται ίσο με το 0.5 του μέτρου ελαστικότητας του υλικού της κολόνας, h είναι το ύψος της κολόνας και Id είναι η στρεπτική ροπή αδράνειας της διατομής. Το Id λαμβάνεται από τον ακόλουθο πίνακα.
Δυστρεψία του διαφραγματικού ορόφου
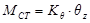 όπου
όπου 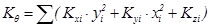 (7’)
(7’)
Η ποσότητα Κθ ονομάζεται δυστρεψία (στροφική δυσκαμψία) του διαφράγματος και έχει μονάδες N·m, κατ’ αναλογία με τις ποσότητες Kx=Σ(Kxi), Ky=Σ(Kyi), οι οποίες ονομάζονται μεταφορικές δυσκαμψίες του διαφράγματος κατά τη διεύθυνση x και y αντίστοιχα και έχουν μονάδες N/m.
Ορισμοί:
Μεταφορική δυσκαμψία Κj διαφράγματος είναι η δύναμη κατά τη διεύθυνση j που απαιτείται για να προκαλέσει σχετική παράλληλη μετατόπιση του διαφράγματος κατά μία μονάδα προς αυτή τη διεύθυνση.
Δυστρεψία Kθ διαφράγματος είναι η ροπή που απαιτείται για να προκαλέσει σχετική στροφή του διαφράγματος κατά μία μονάδα.
Παρατήρηση
Η (ίδια) δυστρεψία των κολονών Kz είναι πολύ μικρή και συνήθως παραλείπεται.
[1] Οι εκκεντρότητες eox, eoy ονομάζονται στατικές, επειδή εξαρτώνται μόνο από τη γεωμετρία του φορέα και καθόλου από την εξωτερική φόρτιση. Όπως θα δούμε στο κεφάλαιο 6, εκτός από τις στατικές εκκεντρότητες, υπάρχουν και οι τυχηματικές εκκεντρότητες.